TL;DR:
We introduce the convolutional VQGAN to combine both the efficiency of convolutional approaches
with the expressive power of transformers, and to combine adversarial with likelihood training
in a perceptually meaningful way.
The VQGAN learns a codebook of context-rich visual parts,
whose composition is then modeled with an autoregressive transformer.
Abstract
Designed to learn long-range interactions on sequential data, transformers continue to show state-of-the-art results on a wide variety of tasks. In contrast to CNNs, they contain no inductive bias that prioritizes local interactions. This makes them expressive, but also computationally infeasible for long sequences, such as high-resolution images. We demonstrate how combining the effectiveness of the inductive bias of CNNs with the expressivity of transformers enables them to model and thereby synthesize high-resolution images. We show how to (i) use CNNs to learn a context-rich vocabulary of image constituents, and in turn (ii) utilize transformers to efficiently model their composition within high-resolution images. Our approach is readily applied to conditional synthesis tasks, where both non-spatial information, such as object classes, and spatial information, such as segmentations, can control the generated image. In particular, we present the first results on semantically-guided synthesis of megapixel images with transformers.
Results
and applications of our model.
Figure 2. Our approach uses a convolutional VQGAN to learn a codebook of context-rich visual parts, whose composition is subsequently modeled with an autoregressive transformer architecture. A discrete codebook provides the interface between these architectures and a patch-based discriminator enables strong compression while retaining high perceptual quality. This method introduces the efficiency of convolutional approaches to transformer based high resolution image synthesis.
Table 1. Comparing Transformer and PixelSNAIL architectures across different datasets and model sizes. For all settings, transformers outperform the state-of-the-art model from the PixelCNN family, PixelSNAIL in terms of NLL. This holds both when comparing NLL at fixed times (PixelSNAIL trains roughly 2 times faster) and when trained for a fixed number of steps. See Sec. 4.1 for the abbreviations.
Figure 5. Samples generated from semantic layouts on S-FLCKR. Sizes from top-to-bottom: 1280 × 832, 1024 × 416 and 1280 × 240 pixels. Best viewed zoomed in. A larger visualization can be found in the appendix, see Fig 13.
Figure 6. Applying the sliding attention window approach (Fig. 3) to various conditional image synthesis tasks. Top: Depth-to-image on RIN, 2nd row: Stochastic superresolution on IN, 3rd and 4th row: Semantic synthesis on S-FLCKR, bottom: Edge-guided synthesis on IN. The resulting images vary between 368 × 496 and 1024× 576, hence they are best viewed zoomed in.
Figure 11. Comparing our approach with the pixel-based approach of [7]. Here, we use our f = 16 S-FLCKR model to obtain high-fidelity image completions of the inputs depicted on the left (half completions). For each conditioning, we show three of our samples (top) and three of [7] (bottom).
Figure 12. Comparing our approach with the pixel-based approach of [7]. Here, we use our f = 16 S-FLCKR model to obtain high-fidelity image completions of the inputs depicted on the left (half completions). For each conditioning, we show three of our samples (top) and three of [7] (bottom).
Figure 4. Transformers within our setting unify a wide range of image synthesis tasks. We show 256 × 256 synthesis results across different conditioning inputs and datasets, all obtained with the same approach to exploit inductive biases of effective CNN based VQGAN architectures in combination with the expressivity of transformer architectures. Top row: Completions from unconditional training on ImageNet. 2nd row: Depth-to-Image on RIN. 3rd row: Semantically guided synthesis on COCO-Stuff (left) and ADE20K (right). 4th row: Pose-guided person generation on DeepFashion. Bottom row: Class-conditional samples on RIN.
Figure 23. Unconditional samples from a model trained on LSUN Churches & Towers, using the sliding attention window.
Figure 13. Samples generated from semantic layouts on S-FLCKR. Sizes from top-to-bottom: 1280 × 832, 1024 × 416 and 1280 × 240 pixels.
Figure 14. Samples generated from semantic layouts on S-FLCKR. Sizes from top-to-bottom: 1536× 512, 1840× 1024, and 1536× 620 pixels.
Figure 15. Samples generated from semantic layouts on S-FLCKR. Sizes from top-to-bottom: 2048× 512, 1460× 440, 2032× 448 and 2016× 672 pixels.
Figure 16. Samples generated from semantic layouts on S-FLCKR. Sizes from top-to-bottom: 1280 × 832, 1024 × 416 and 1280 × 240 pixels.
Figure 17. Depth-guided neural rendering on RIN with f = 16 using the sliding attention window.
Figure 18. Depth-guided neural rendering on RIN with f = 16 using the sliding attention window.
Figure 19. Intentionally limiting the receptive field can lead to interesting creative applications like this one: Edge-to-Image synthesis on IN with f = 8, using the sliding attention window.
Figure 20. Additional results for stochastic superresolution with an f = 16 model on IN, using the sliding attention window.
Figure 21. Samples generated from semantic layouts on S-FLCKR with f = 16, using the sliding attention window.
Figure 22. Samples generated from semantic layouts on S-FLCKR with f = 32, using the sliding attention window.
Figure 7. Evaluating the importance of effective codebook for HQ-Faces (CelebA-HQ and FFHQ) for a fixed sequence length |s|= 16·16 = 256. Globally consistent structures can only be modeled with a context-rich vocabulary (right). All samples are generated with temperature t = 1.0 and top-k sampling with k = 100. Last row reports the speedup over the f1 baseline which operates directly on pixels and takes 7258 seconds to produce a sample on a NVIDIA GeForce GTX Titan X.
Figure 8. Trade-off between negative log-likelihood (nll) and reconstruction error. While context-rich encodings obtained with large factors f allow the transformer to effectively model long-range interactions, the reconstructions capabilities and hence quality of samples suffer after a critical value (here, f = 16). For more details, see Sec. B.
Figure 9. We compare the ability of VQVAEs and VQGANs to learn perceptually rich encodings, which allow for high-fidelity reconstructions with large factors f . Here, using the same architecture and f = 16, VQVAE reconstructions are blurry and contain little information about the image, whereas VQGAN recovers images faithfully. See also Sec. B.
Figure 10. Samples on landscape dataset (left) obtained with different factors f , analogous to Fig. 7. In contrast to faces, a factor of f = 32 still allows for faithful reconstructions (right). See also Sec. B.
Figure 24. Additional 256× 256 results on the ADE20K dataset.
Figure 25. Additional 256× 256 results on the COCO-Stuff dataset.
Figure 26. Conditional samples for the depth-to-image model on IN.
Figure 27. Conditional samples for the pose-guided synthesis model via keypoints on DeepFashion.
Figure 28. Samples produced by the class-conditional model trained on RIN.
Figure 29. Samples synthesized by the class-conditional IN model.
Figure 30. Top: All sequence permutations we investigate, illustrated on a 4× 4 grid. Bottom: The transformer architecture is permutation invariant but next-token prediction is not: The average loss on the validation split of ImageNet, corresponding to the negative log-likelihood, differs significantly between different prediction orderings. Among our choices, the commonly used row-major order performs best.
Figure 31. Random samples from transformer models trained with different orderings for autoregressive prediction as described in Sec. 4.4.
Related Work on Modular Compositions of Deep Learning Models
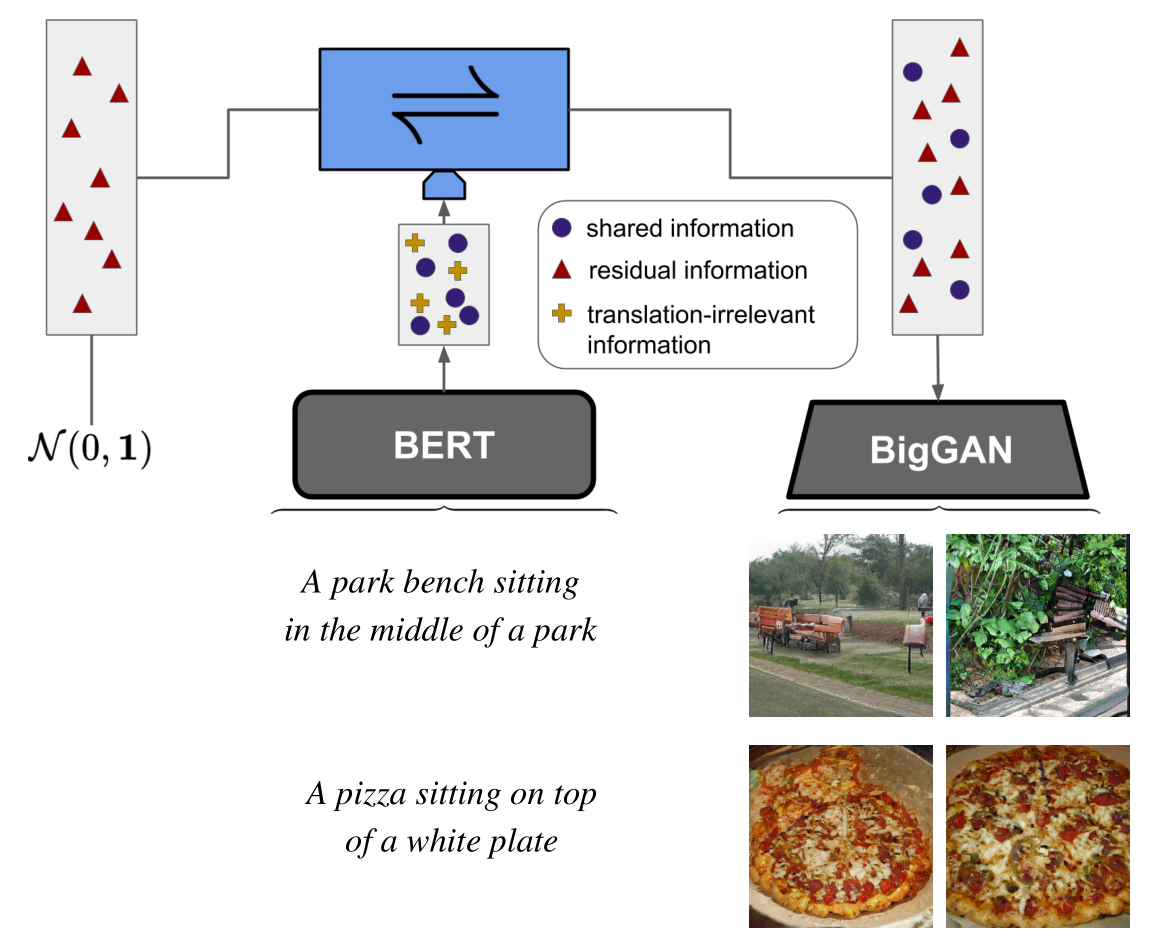
Given the ever-increasing computational costs of modern machine learning models, we need to find new ways to reuse such expert models and thus tap into the resources that have been invested in their creation. Recent work suggests that the power of these massive models is captured by the representations they learn. Therefore, we seek a model that can relate between different existing representations and propose to solve this task with a conditionally invertible network. This network demonstrates its capability by (i) providing generic transfer between diverse domains, (ii) enabling controlled content synthesis by allowing modification in other domains, and (iii) facilitating diagnosis of existing representations by translating them into interpretable domains such as images. Our domain transfer network can translate between fixed representations without having to learn or finetune them. This allows users to utilize various existing domain-specific expert models from the literature that had been trained with extensive computational resources. Experiments on diverse conditional image synthesis tasks, competitive image modification results and experiments on image-to-image and text-to-image generation demonstrate the generic applicability of our approach. For example, we translate between BERT and BigGAN, state-of-the-art text and image models to provide text-to-image generation, which neither of both experts can perform on their own.
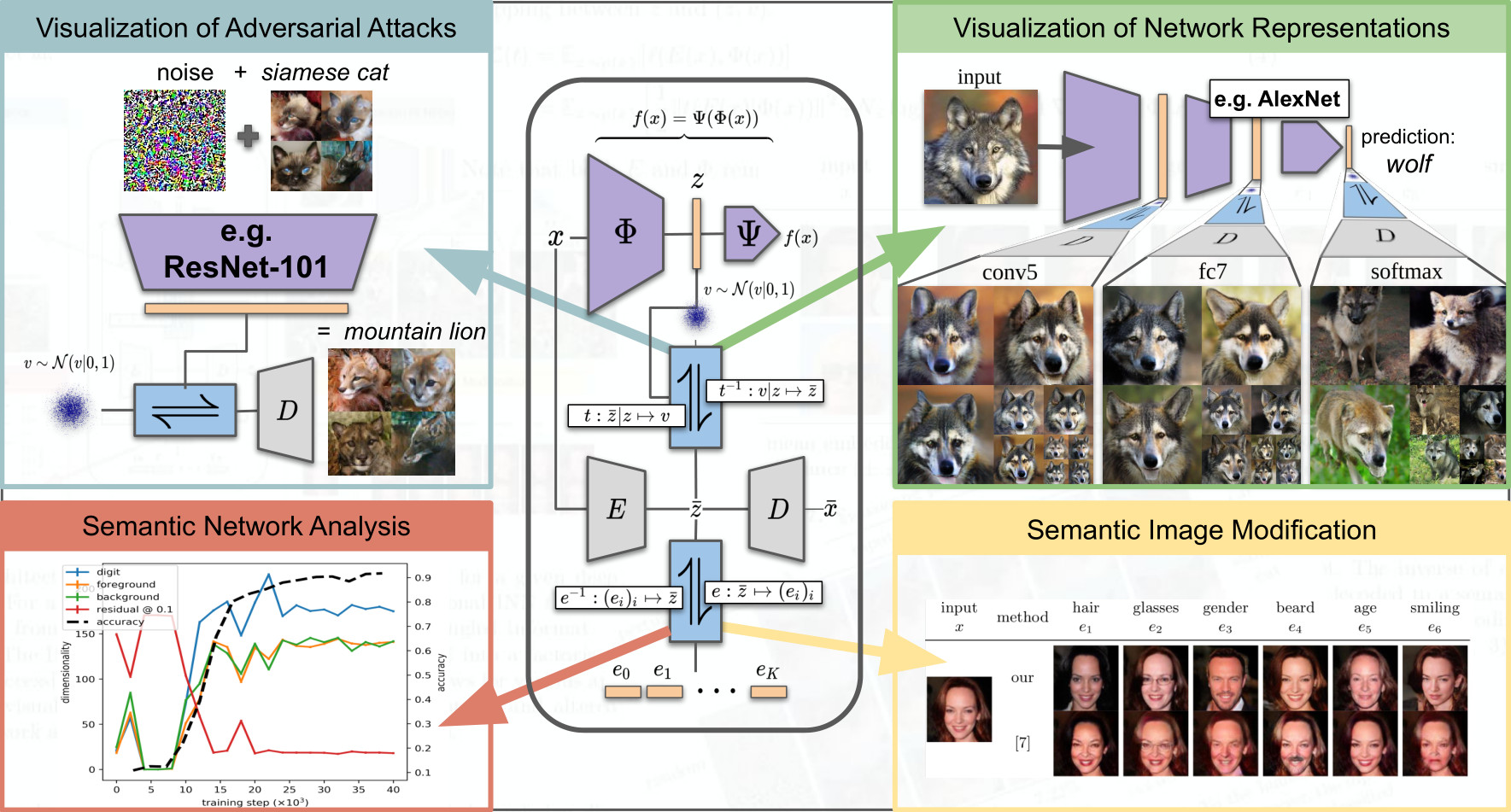
To tackle increasingly complex tasks, it has become an essential ability of neural networks to learn abstract representations. These task-specific representations and, particularly, the invariances they capture turn neural networks into black box models that lack interpretability. To open such a black box, it is, therefore, crucial to uncover the different semantic concepts a model has learned as well as those that it has learned to be invariant to. We present an approach based on INNs that (i) recovers the task-specific, learned invariances by disentangling the remaining factor of variation in the data and that (ii) invertibly transforms these recovered invariances combined with the model representation into an equally expressive one with accessible semantic concepts. As a consequence, neural network representations become understandable by providing the means to (i) expose their semantic meaning, (ii) semantically modify a representation, and (iii) visualize individual learned semantic concepts and invariances. Our invertible approach significantly extends the abilities to understand black box models by enabling post-hoc interpretations of state-of-the-art networks without compromising their performance.
Acknowledgement
This page is based on a design by TEMPLATED.