Abstract
Neural networks have greatly boosted performance in computer vision by learning powerful representations of input data. The drawback of end-to-end training for maximal overall performance are black-box models whose hidden representations are lacking interpretability: Since distributed coding is optimal for latent layers to improve their robustness, attributing meaning to parts of a hidden feature vector or to individual neurons is hindered. We formulate interpretation as a translation of hidden representations onto semantic concepts that are comprehensible to the user. The mapping between both domains has to be bijective so that semantic modifications in the target domain correctly alter the original representation. The proposed invertible interpretation network can be transparently applied on top of existing architectures with no need to modify or retrain them. Consequently, we translate an original representation to an equivalent yet interpretable one and backwards without affecting the expressiveness and performance of the original. The invertible interpretation network disentangles the hidden representation into separate, semantically meaningful concepts. Moreover, we present an efficient approach to define semantic concepts by only sketching two images and also an unsupervised strategy. Experimental evaluation demonstrates the wide applicability to interpretation of existing classification and image generation networks as well as to semantically guided image manipulation.
New Works on Understanding and Disentangling Latent Representations with INNs
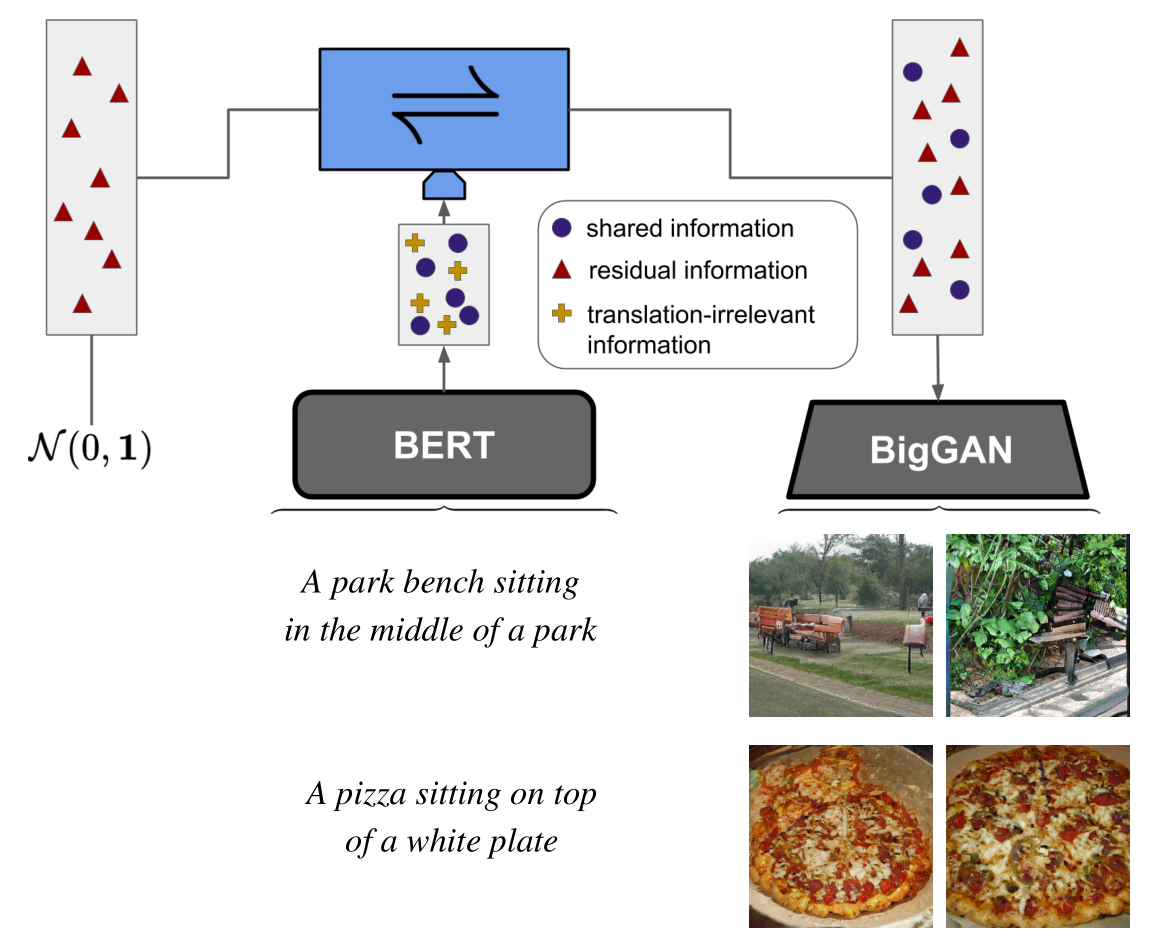
Given the ever-increasing computational costs of modern machine learning models, we need to find new ways to reuse such expert models and thus tap into the resources that have been invested in their creation. Recent work suggests that the power of these massive models is captured by the representations they learn. Therefore, we seek a model that can relate between different existing representations and propose to solve this task with a conditionally invertible network. This network demonstrates its capability by (i) providing generic transfer between diverse domains, (ii) enabling controlled content synthesis by allowing modification in other domains, and (iii) facilitating diagnosis of existing representations by translating them into interpretable domains such as images. Our domain transfer network can translate between fixed representations without having to learn or finetune them. This allows users to utilize various existing domain-specific expert models from the literature that had been trained with extensive computational resources. Experiments on diverse conditional image synthesis tasks, competitive image modification results and experiments on image-to-image and text-to-image generation demonstrate the generic applicability of our approach. For example, we translate between BERT and BigGAN, state-of-the-art text and image models to provide text-to-image generation, which neither of both experts can perform on their own.
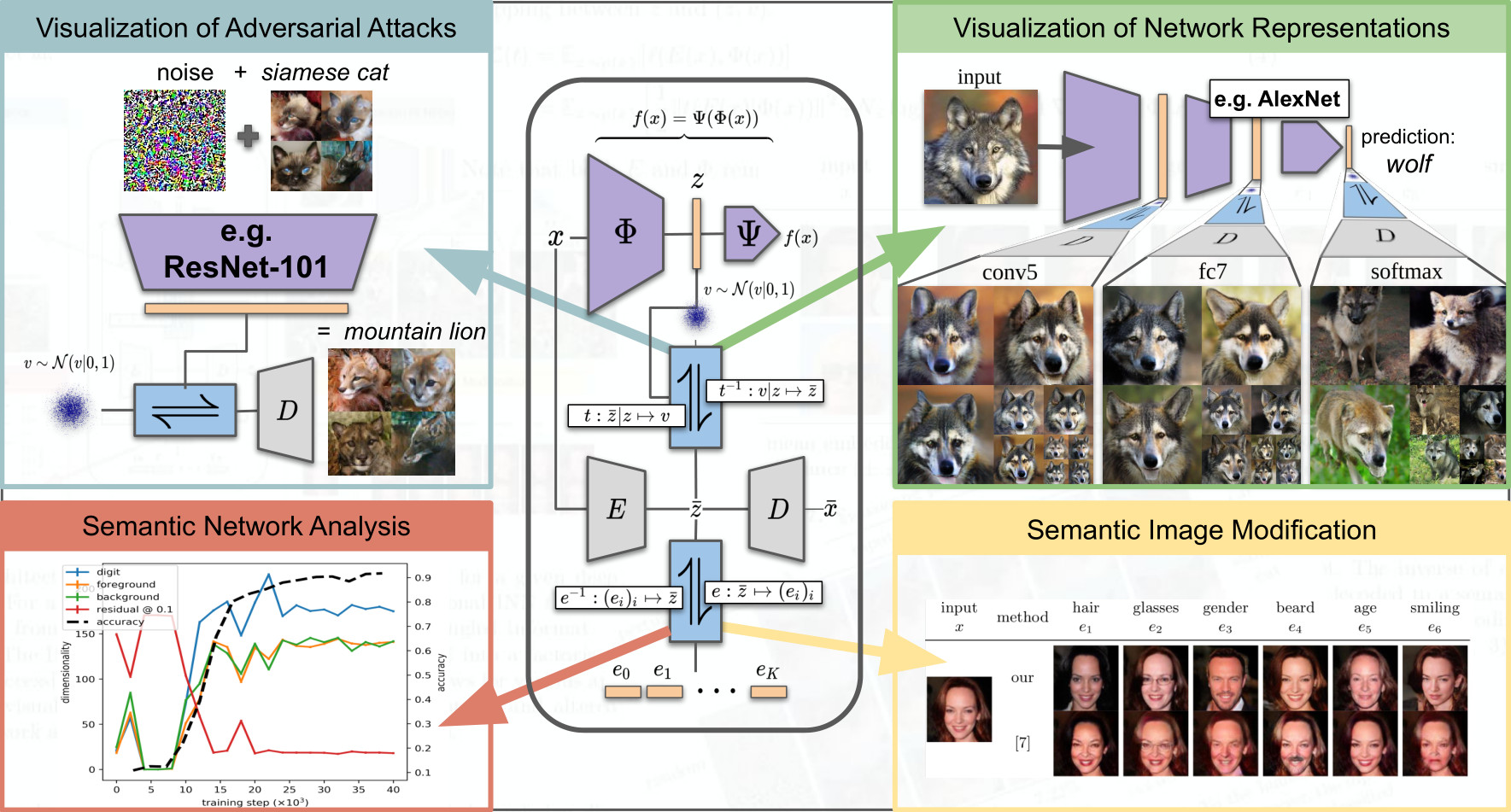
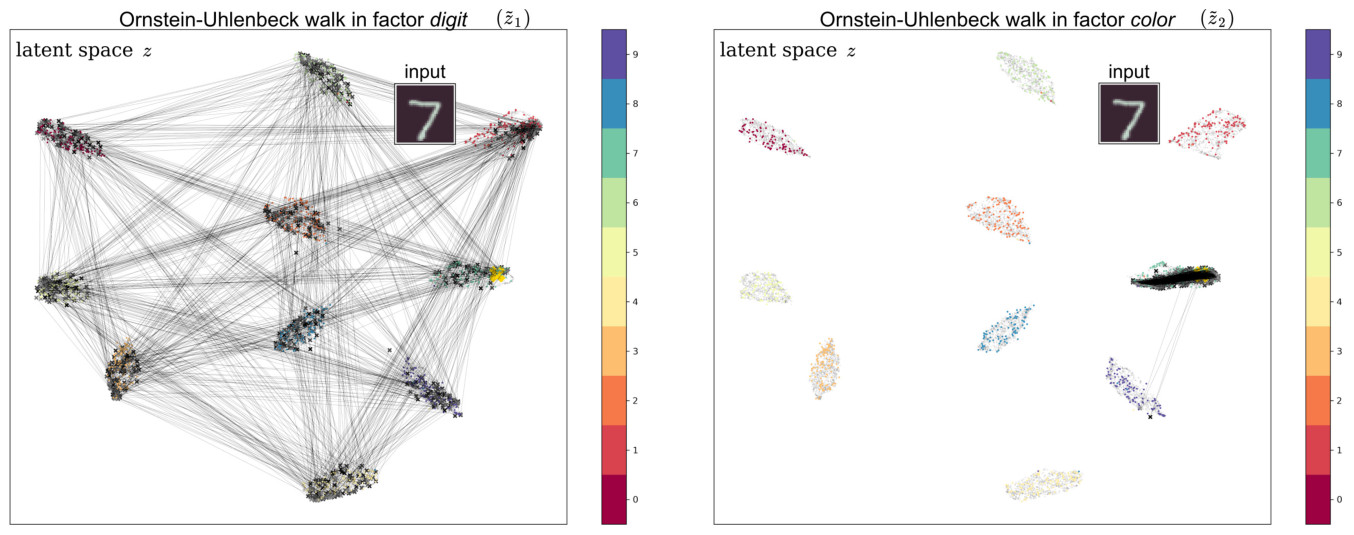
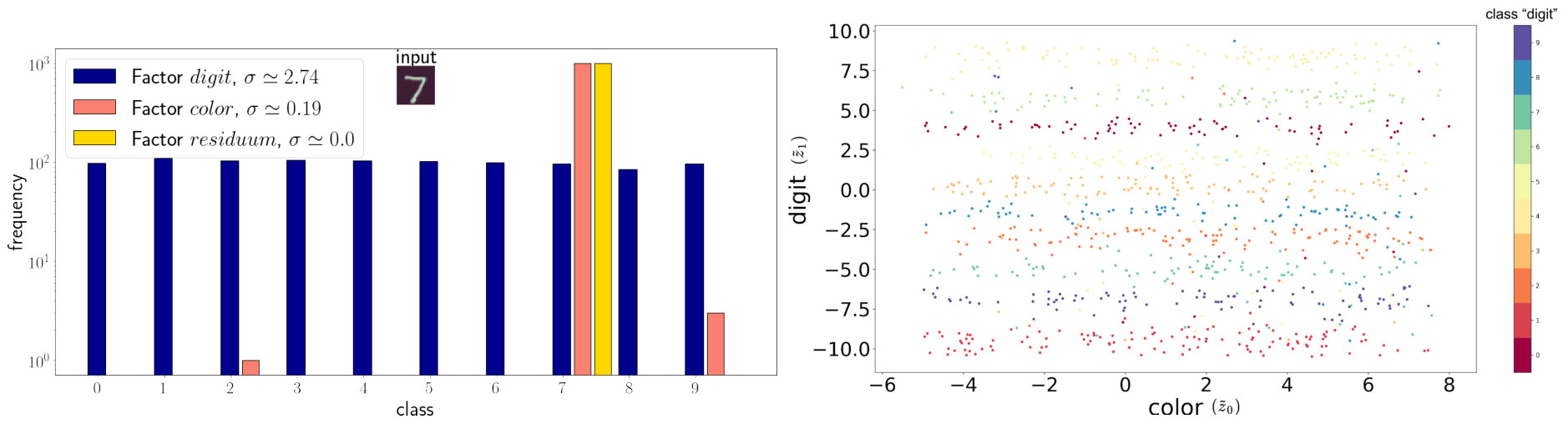
To tackle increasingly complex tasks, it has become an essential ability of neural networks to learn abstract representations. These task-specific representations and, particularly, the invariances they capture turn neural networks into black box models that lack interpretability. To open such a black box, it is, therefore, crucial to uncover the different semantic concepts a model has learned as well as those that it has learned to be invariant to. We present an approach based on INNs that (i) recovers the task-specific, learned invariances by disentangling the remaining factor of variation in the data and that (ii) invertibly transforms these recovered invariances combined with the model representation into an equally expressive one with accessible semantic concepts. As a consequence, neural network representations become understandable by providing the means to (i) expose their semantic meaning, (ii) semantically modify a representation, and (iii) visualize individual learned semantic concepts and invariances. Our invertible approach significantly extends the abilities to understand black box models by enabling post-hoc interpretations of state-of-the-art networks without compromising their performance.
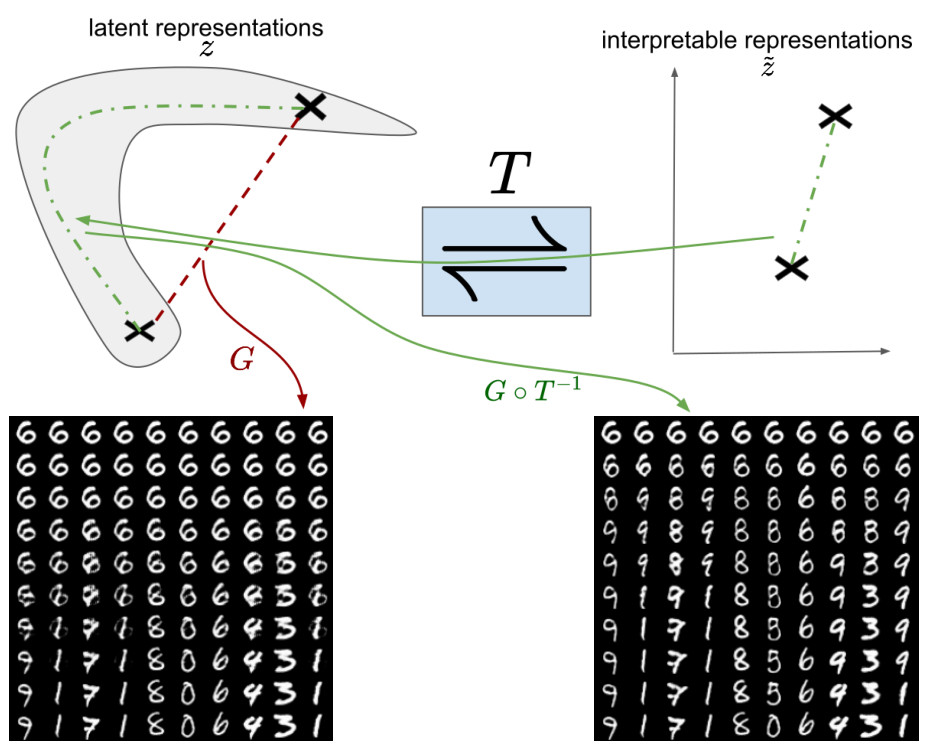
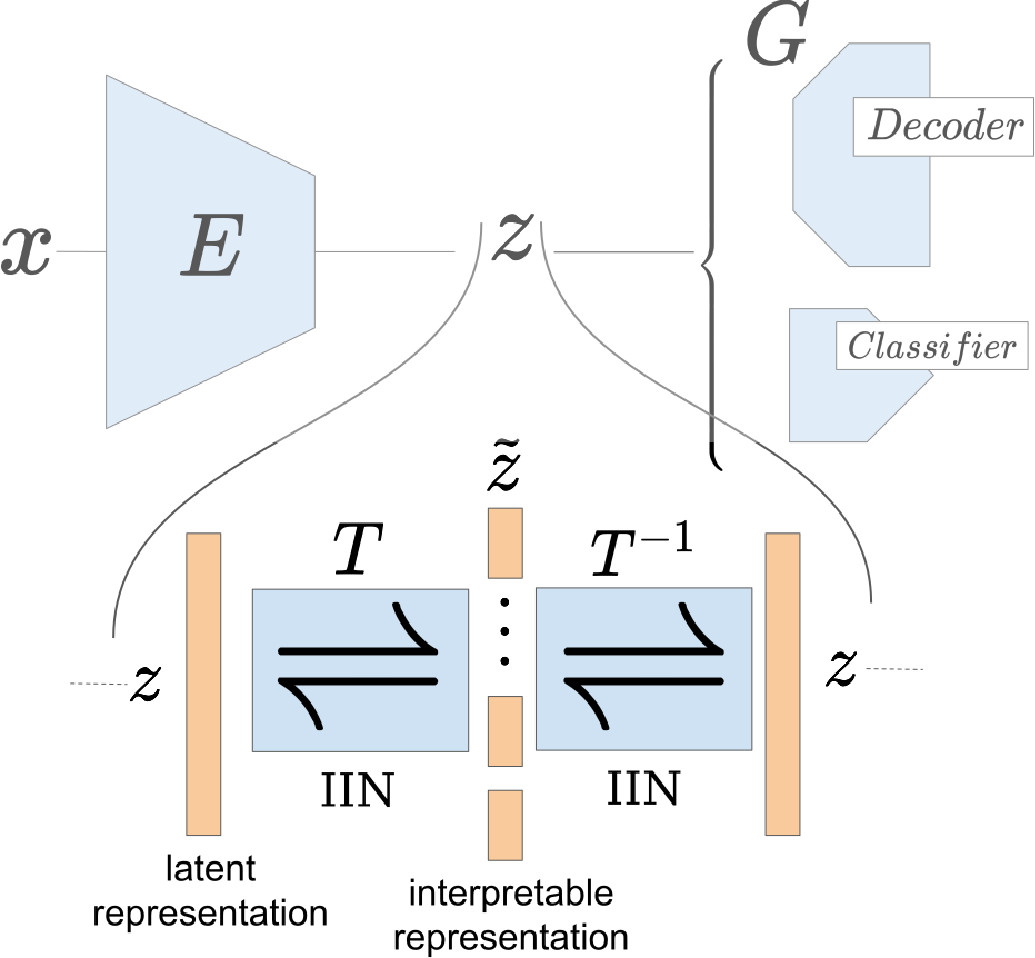 Our Invertible Interpretation Network T can be applied
to arbitrary existing models. Its invertibility
guarantees that the translation from z to
z̃ does
not affect the performance of the model to be
interpreted.
Our Invertible Interpretation Network T can be applied
to arbitrary existing models. Its invertibility
guarantees that the translation from z to
z̃ does
not affect the performance of the model to be
interpreted.