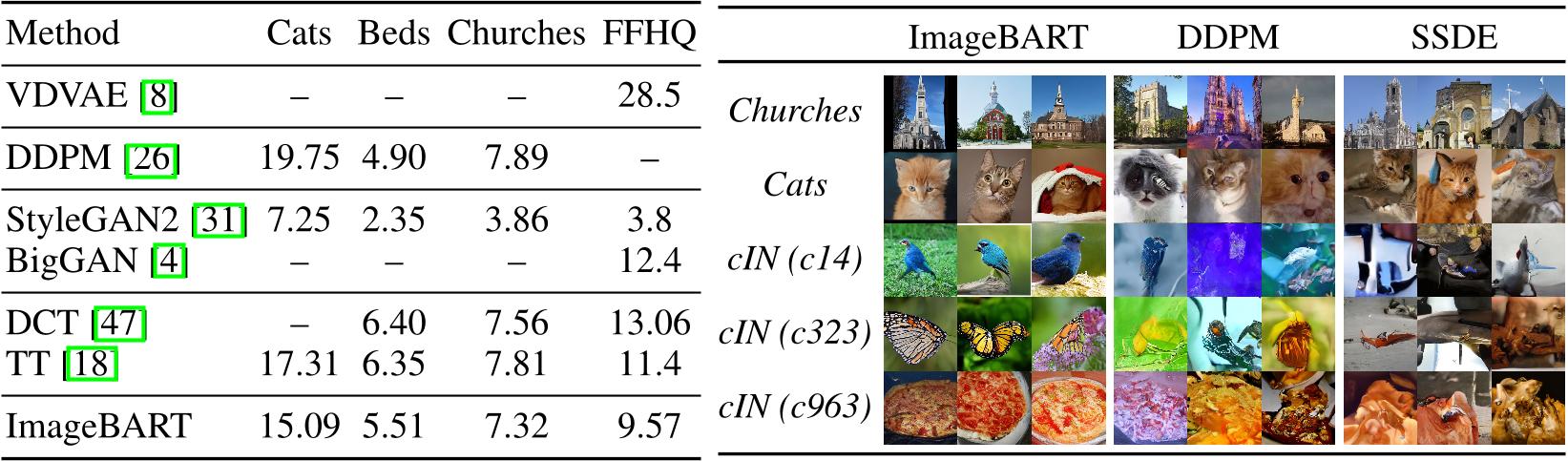
Abstract
Autoregressive models and their sequential factorization of the data likelihood have recently demonstrated great potential for image representation and synthesis. Nevertheless, they incorporate image context in a linear 1D order by attending only to previously synthesized image patches above or to the left. Not only is this unidirectional, sequential bias of attention unnatural for images as it disregards large parts of a scene until synthesis is almost complete. It also processes the entire image on a single scale, thus ignoring more global contextual information up to the gist of the entire scene. As a remedy we incorporate a coarse-to-fine hierarchy of context by combining the autoregressive formulation with a multinomial diffusion process: Whereas a multistage diffusion process successively removes information to coarsen an image, we train a (short) Markov chain to invert this process. In each stage, the resulting autoregressive ImageBART model progressively incorporates context from previous stages in a coarse-to-fine manner. Experiments show greatly improved image modification capabilities over autoregressive models while also providing high-fidelity image generation, both of which are enabled through efficient training in a compressed latent space. Specifically, our approach can take unrestricted, user-provided masks into account to perform local image editing. Thus, in contrast to pure autoregressive models, it can solve free-form image inpainting and, in the case of conditional models, local, text-guided image modification without requiring mask-specific training.
Results
and applications of our model.
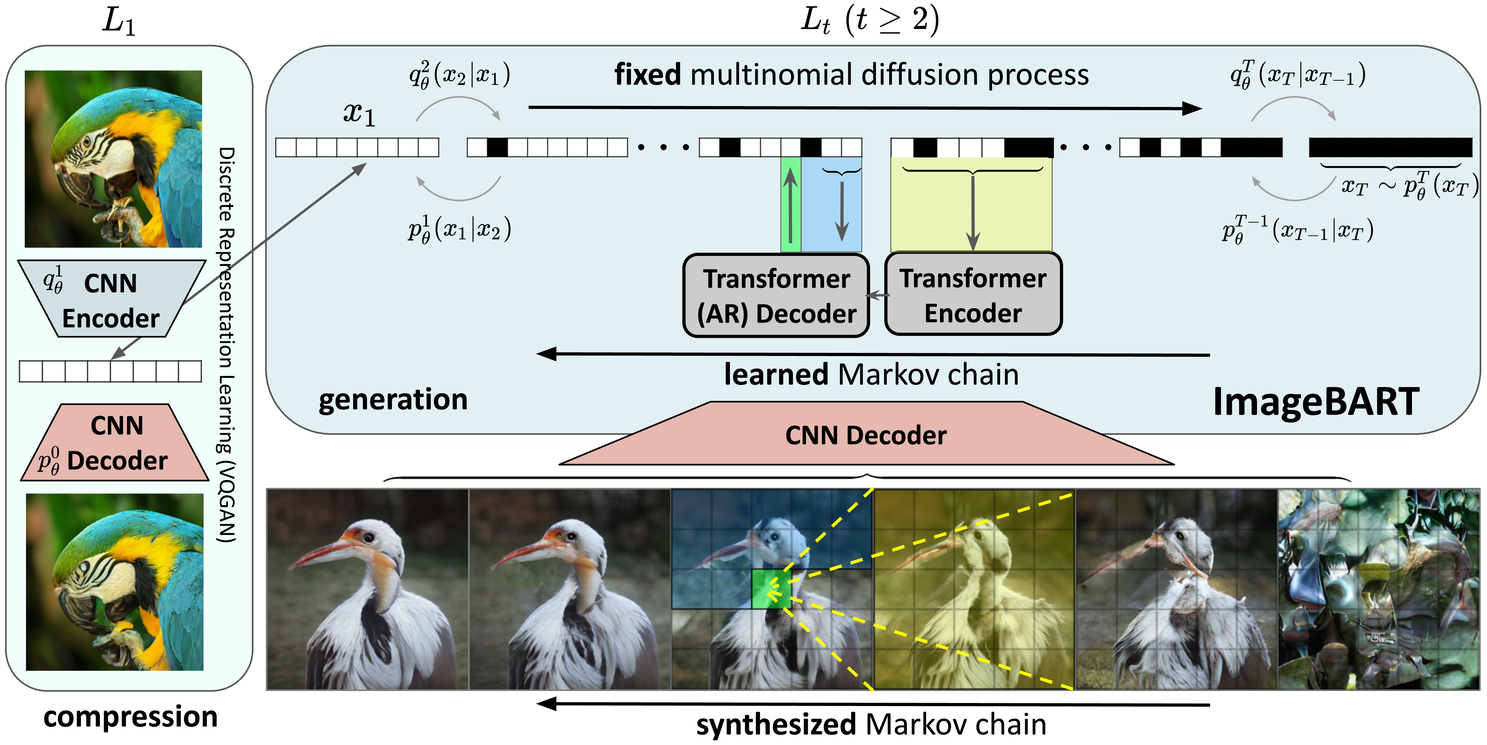
 Figure 1: We first learn a compressed, discrete image representation x1 and subsequently our generative ImageBART model reverts a fixed multinomial diffusion process via a Markov Chain, where the individual transition probabilities are modeled as independent autoregressive encoder-decoder models. This introduces a coarse-to-fine hierarchy such that each individual AR model can attend to global context from its preceding scale in the hierarchy.
Figure 1: We first learn a compressed, discrete image representation x1 and subsequently our generative ImageBART model reverts a fixed multinomial diffusion process via a Markov Chain, where the individual transition probabilities are modeled as independent autoregressive encoder-decoder models. This introduces a coarse-to-fine hierarchy such that each individual AR model can attend to global context from its preceding scale in the hierarchy.
 Table 2: Quantitative analysis on conditional models. Left: Results on class conditional Imagenet for different rejection rates, see also Fig, 20 in the supplemental. Right: Results of text-conditional ImageBART and comparison with TT [18] on the CC test set. Corresponding qualitative comparisons can be found in Fig. 21.
Table 2: Quantitative analysis on conditional models. Left: Results on class conditional Imagenet for different rejection rates, see also Fig, 20 in the supplemental. Right: Results of text-conditional ImageBART and comparison with TT [18] on the CC test set. Corresponding qualitative comparisons can be found in Fig. 21.
 Table 3: Assessing the effect of different T with a fixed number of parameters distributed equally over all scales. All models are trained on FFHQ. Left: Full image generation results. Right: Using the example of upper image completion, we evaluate the ability to complete and modifiy an image, see Sec. 4.3 and 4.4.
Table 3: Assessing the effect of different T with a fixed number of parameters distributed equally over all scales. All models are trained on FFHQ. Left: Full image generation results. Right: Using the example of upper image completion, we evaluate the ability to complete and modifiy an image, see Sec. 4.3 and 4.4.
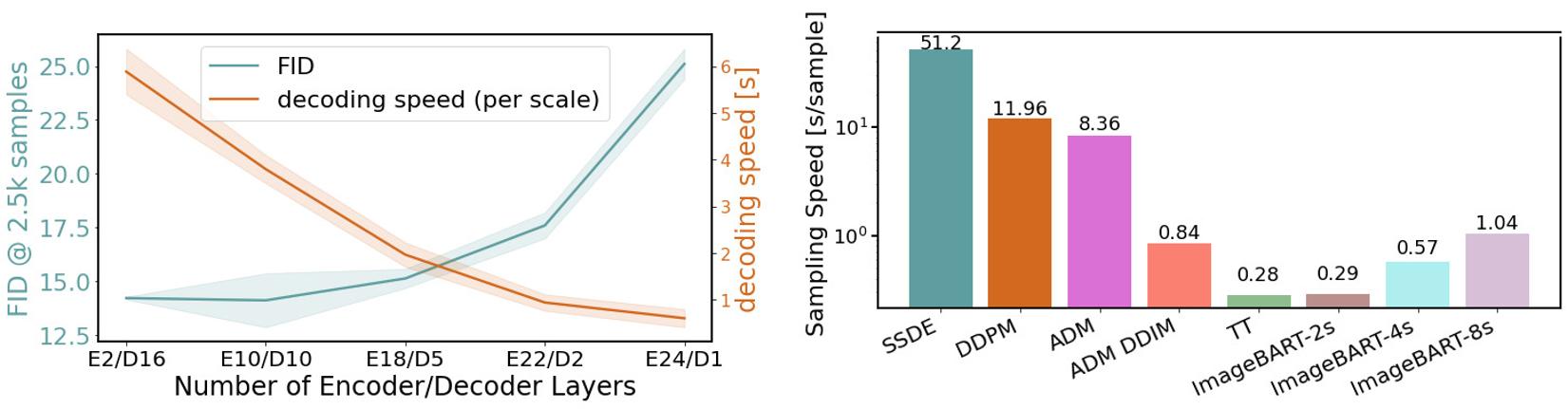 Figure 8: Left: Effect of number of encoder vs. decoder layers for a fixed total number of model parameters, evaluated on LSUN-Churches. Right: Our model achieves better sampling performance than state of the art diffusion models (SSDE [65], DDPM [26], ADM [13]) and also approaches the inference speed of TT [18], which only consists of a single autoregressive stage. Reducing the number of scales increases inference speed at the expense of controllability.
Figure 8: Left: Effect of number of encoder vs. decoder layers for a fixed total number of model parameters, evaluated on LSUN-Churches. Right: Our model achieves better sampling performance than state of the art diffusion models (SSDE [65], DDPM [26], ADM [13]) and also approaches the inference speed of TT [18], which only consists of a single autoregressive stage. Reducing the number of scales increases inference speed at the expense of controllability.
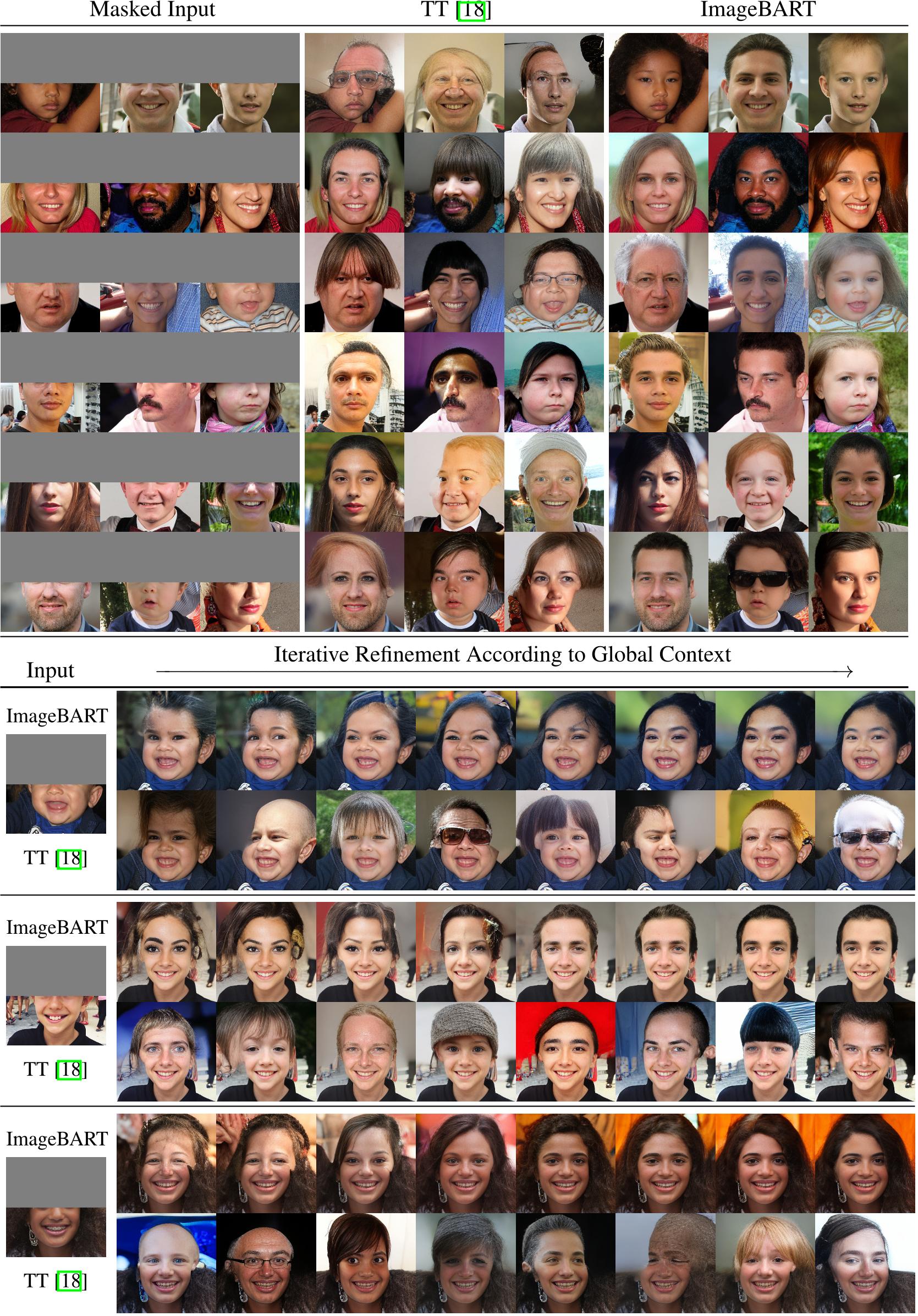 Figure 14: Additional examples for upper half completion as in Fig. 5. The top shows masked inputs, results by TT [18] and results by ImageBART. The bottom shows every other sample of the forward-backward chain described in Sec. 4.3 and Sec. A.3. ImageBART can incorporate global context to produce consistent completions, whereas TT is limited to context from above and thus fails to produce consistent completions.
Figure 14: Additional examples for upper half completion as in Fig. 5. The top shows masked inputs, results by TT [18] and results by ImageBART. The bottom shows every other sample of the forward-backward chain described in Sec. 4.3 and Sec. A.3. ImageBART can incorporate global context to produce consistent completions, whereas TT is limited to context from above and thus fails to produce consistent completions.
 Figure 26: Nearest neighbors to samples from ImageBART from the FFHQ train set measured by averaging over different feature layers of a VGG-16 trained on ImageNet. The first example in each row shows a generated sample from our model. The remaining ones depict the corresponding nearest neighbors in ascending order.
Figure 26: Nearest neighbors to samples from ImageBART from the FFHQ train set measured by averaging over different feature layers of a VGG-16 trained on ImageNet. The first example in each row shows a generated sample from our model. The remaining ones depict the corresponding nearest neighbors in ascending order.
 Figure 27: Nearest neighbors to samples from ImageBART from the LSUN-churches train set measured by averaging over different feature layers of a VGG-16 trained on ImageNet. The first example in each row shows a generated sample from our model. The remaining ones depict the corresponding nearest neighbors in ascending order.
Figure 27: Nearest neighbors to samples from ImageBART from the LSUN-churches train set measured by averaging over different feature layers of a VGG-16 trained on ImageNet. The first example in each row shows a generated sample from our model. The remaining ones depict the corresponding nearest neighbors in ascending order.